自动微分¶

在训练神经网络时，最常用的算法是**反向传播**。在这个算法中，参数（模型权重）根据损失函数相对于给定参数的**梯度**进行调整。

为了计算这些梯度，PyTorch 提供了一个内置的微分引擎，称为 torch.autograd。它支持对任何计算图自动计算梯度。

考虑最简单的单层神经网络，具有输入 x、参数 w 和 b，以及一些损失函数。可以在 PyTorch 中按以下方式定义它：

import torch

x = torch.ones(5)  # input tensor
y = torch.zeros(3)  # expected output
w = torch.randn(5, 3, requires_grad=True)
b = torch.randn(3, requires_grad=True)
z = torch.matmul(x, w)+b
loss = torch.nn.functional.binary_cross_entropy_with_logits(z, y)

张量、函数和计算图¶

这段代码定义了以下**计算图**:

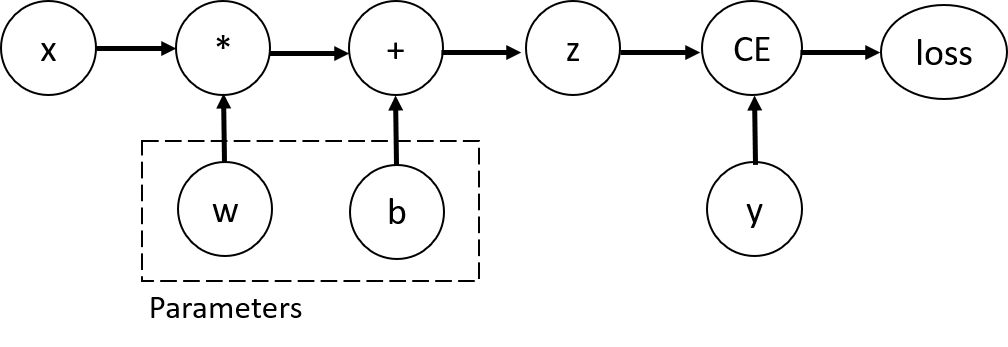
在这个网络中，w 和 b 是**参数**，我们需要对它们进行优化。因此，我们需要能够计算损失函数相对于这些变量的梯度。为了做到这一点，我们设置了这些张量的 requires_grad 属性。

或在创建后使用 x.requires_grad_(True) 方法来设置。

我们应用于张量以构建计算图的函数实际上是 Function 类的对象。这个对象知道如何在*前向*方向计算函数，也知道如何在*反向传播*步骤中计算其导数。对于反向传播函数的引用存储在张量的 grad_fn` 属性中。您可以在`文档 <https://pytorch.org/docs/stable/autograd.html#function>`__ 中找到有关 Function 的更多信息。

print(f"Gradient function for z = {z.grad_fn}")
print(f"Gradient function for loss = {loss.grad_fn}")

计算梯度¶

为了优化神经网络中的参数权重，我们需要计算损失函数相对于参数的导数，即在某些固定的 x 和 y 值下，我们需要 frac{partial loss}{partial w} 和 frac{partial loss}{partial b}。要计算这些导数，我们调用 loss.backward()，然后从 w.grad 和 b.grad 中检索值：

loss.backward()
print(w.grad)
print(b.grad)

禁用梯度跟踪¶

默认情况下，所有具有 requires_grad=True 的张量都在跟踪它们的计算历史并支持梯度计算。然而，有些情况下我们不需要这样做，例如，当我们已经训练好模型并只想将其应用于一些输入数据时，即我们只想通过网络进行*前向*计算。我们可以通过将我们的计算代码包裹在 torch.no_grad() 块中来停止跟踪计算：

z = torch.matmul(x, w)+b
print(z.requires_grad)

with torch.no_grad():
    z = torch.matmul(x, w)+b
print(z.requires_grad)

另一种实现相同结果的方法是对张量使用 detach() 方法：

z = torch.matmul(x, w)+b
z_det = z.detach()
print(z_det.requires_grad)

希望禁用梯度跟踪的原因可能如下： - 将神经网络中的某些参数标记为**冻结参数**。 - 在仅进行前向传递时**加速计算**，因为不跟踪梯度的张量上的计算会更高效。

可选阅读：张量梯度(Tensor Gradients)和雅可比乘积(Jacobian Products)¶

在很多情况下，我们有一个标量损失函数，需要计算相对于某些参数的梯度。然而，也有一些情况下，输出函数是一个任意的张量。在这种情况下，PyTorch 允许您计算所谓的**雅可比乘积**，而不是实际的梯度。

For a vector function \(\vec{y}=f(\vec{x})\), where \(\vec{x}=\langle x_1,\dots,x_n\rangle\) and \(\vec{y}=\langle y_1,\dots,y_m\rangle\), a gradient of \(\vec{y}\) with respect to \(\vec{x}\) is given by Jacobian matrix:

\[J=\left(\begin{array}{ccc} \frac{\partial y_{1}}{\partial x_{1}} & \cdots & \frac{\partial y_{1}}{\partial x_{n}}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{array}\right)\]

Instead of computing the Jacobian matrix itself, PyTorch allows you to compute Jacobian Product \(v^T\cdot J\) for a given input vector \(v=(v_1 \dots v_m)\). This is achieved by calling backward with \(v\) as an argument. The size of \(v\) should be the same as the size of the original tensor, with respect to which we want to compute the product:

inp = torch.eye(4, 5, requires_grad=True)
out = (inp+1).pow(2).t()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"First call\n{inp.grad}")
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nSecond call\n{inp.grad}")
inp.grad.zero_()
out.backward(torch.ones_like(out), retain_graph=True)
print(f"\nCall after zeroing gradients\n{inp.grad}")

Notice that when we call backward for the second time with the same argument, the value of the gradient is different. This happens because when doing backward propagation, PyTorch accumulates the gradients, i.e. the value of computed gradients is added to the grad property of all leaf nodes of computational graph. If you want to compute the proper gradients, you need to zero out the grad property before. In real-life training an optimizer helps us to do this.

Note

Previously we were calling backward() function without parameters. This is essentially equivalent to calling backward(torch.tensor(1.0)), which is a useful way to compute the gradients in case of a scalar-valued function, such as loss during neural network training.

自动微分¶

张量、函数和计算图¶

计算梯度¶

禁用梯度跟踪¶

更多关于计算图¶

可选阅读：张量梯度(Tensor Gradients)和雅可比乘积(Jacobian Products)¶

Further Reading¶

Docs

Tutorials

Resources